Here we are less interested in the definition of the limit than in how to calculate them. We proceed by examples, using the following terminology

f(x) is the function, with all possible x values the domain of the function, all possible y values the range of the function

x₀ is our fixed point, can be finite or infinite, but must be in the domain of the function

y₀ is the limit, can be finite, infinite, or non-existent, if it exists, it must be in the range of the function

Find the limit

Clearly we'll have problems just substituting x = 1, since that will make the denominator zero, and the entire expression undefined.  Instead, we'll do some algebra first to see if we can trim off any fat.  Since (see algebra formulae)

We can write

And so

Find the limit

Again, straight substitution won't work. In fact, regardless of how we play with this limit, we will still have a factor in the denominator which is zero, while the numerator is not. This limit does not exist. We cannot even assign it either +/- infinity, since the answer will be different depending on whether x approaches 4 from below (negative infinity) or above (positive infinity).

Find the limit

Apply the same algebra technique as the first example above, twice:

So,

Find the limit

A little algebra reveals that this limit is also not what it seems

And so

Since 2 is not a function of x, it doesn't matter what the fixed point is, the answer is still 2!

Find the limit

For the three cases: m > n, m = n, m < n.

The m = n case is trivial

In the case where m < n or m > n, from the algebra formulae

So,

Notice that this agrees with the trivial result when m = n.

Find the limit

Multiply by 1 in the form of the numerator with a "+" sign substituted for a "-" sign:

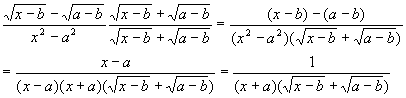
Therefore,

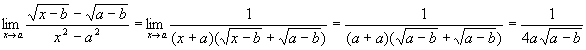
Please note in the above examples that, once the limit has been taken, the limit symbol is removed and the fixed point is substituted for x. Prior to that, the limit symbol is needed. When we are doing pure algebra, we leave off the limit symbol to avoid cluttering the math.

Find the limit

Inspection of the denominator shows it becomes zero at x = 1, which means (x - 1) is a factor of the polynomial in the denominator. Performing a division (you can do the subtraction under the divisor if you like - you will need to be able to factor cubic polynomials like this),

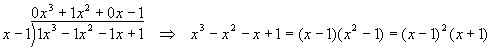
Since x = 1 is an interesting point for the denominator, we can try it with the numerator

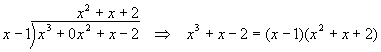
The quadratic term on the right is irreducible, since

So, out limit becomes

The numerator becomes finite while the denominator goes to zero, there is no more algebra which can reduce the expression, so this limit does not exist.

Find the limit

Solution

Here it helps to do a substitution

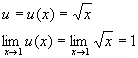
so that we can now write the limit expression as

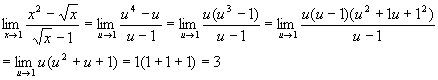
This technique will prove very useful for calculus problems later.