
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Trigonometric Functions of Common Angles The Unit Circle · Degrees and Radians · Quadrants · Common Acute Angles and Right Triangles · A few additional facts about triangles · Recommended Books The Unit CircleThe fundamental ideas needed to understand sines and cosines can be put into one graph, the unit circle:
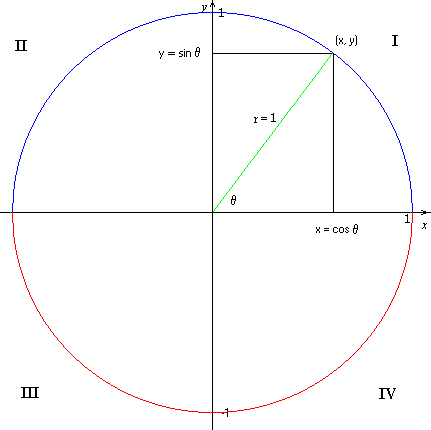
Here we have a circle of radius r = 1 (hence "unit circle"), a point (x, y) on that circle, and perpendiculars from the point to the x and y axes. The line from the origin (0, 0) to the point (x, y) is considered a vector and is usually just labeled with the endpoint (x, y). This vector forms an angle q (Greek theta) with the x-axis. The line segment from (0, 0) to (x, y) is the longest of the three sides of the triangle and is called the hypotenuse. Notice that the point on the x-axis where the perpendicular meets the axis is marked "x = cos q" and the corresponding point on the y-axis is marked "y = sin q". These two points represent the meaning of the sine and cosine of the angle, normally understood as the adjacent and opposite respectively.
Angles are given either in degrees (1 complete circle = 360o) or radians (1 complete circle = 2p). For pure mathematics, radians are preferred, although both measures of angles are in very common use. Generally speaking, when we are interested in sine and cosine as functions (of the angle q), we use radians. Radians are pure numbers, the same as 0, 1, 4.3874653 and p = 3.14159…, while degrees carry units (denoted with the degree sign o). Degrees require special handling – if you use a calculator to calculate the value of trig functions of an angle, you have to make sure you tell your calculator which units, degrees or radians, you are using before you do the calculation.
It is reasonably easy to convert between degrees and radians. We gave the number of each unit in one complete circle above, so:
![]()
Thus, to convert degrees to radians, multiply by
![]()
To convert radians to degrees, multiply by
![]()
Example
Convert 14o to radians.
Solution
Using the first of the two conversion factors above,
![]()
Two details should be pointed out here.
The first is that we did not write "radians" after the answer – the lack of units is typical of pure numbers and is deliberate. If we know the number is an angle and there is no degree sign after it, the likelihood is that the angle has been expressed in radians. The presence of p in the expression is another clue that the angle is expressed in radians. This is an irrational number, and expressing it exactly requires that it be in terms of a multiple of p.
The second detail is how we did the calculation – notice that the degree sign appears once in the numerator (we deliberately expressed 14 as the improper fraction 14/1 to give it an explicit denominator) and once in the denominator. The degrees cancel out – a valuable memory aid for those of us who can’t remember which conversion factor to use!
Example
Convert 3p/4 to degrees.
Solution
Using the second of the two conversion factors above,
![]()
Notice that angles in radians are most often expressed as multiples of p, which helps us decide which conversion factor to use. The important point is that we wanted our answer to be in degrees, which meant that the degree unit needed to be in the numerator. It is possible for us to talk about angles in radians which are not expressed as multiples of p, but in practice such angles occur infrequently.
The coordinate system (also known as the x-y plane) is divided into four regions, or quadrants:
| Quadrant | Allowed angles q (min, max) in degrees; radians | Allowed values of x = cos q | Allowed values of y = sin q |
| I | (0, 90); (0, p/2) | x ³ 0 | y ³ 0 |
| II | (90, 180); (p/2, p) | x £ 0 | y ³ 0 |
| III | (180, 270); (p, 3p/2) | x £ 0 | y £ 0 |
| IV | (270, 360); (3p/2, 2p) | x ³ 0 | y £ 0 |
(x, y) = (1, 0): Angle with the x-axis: q = 0
Þ cos q = cos 0 = 1; sin q = sin 0 = 0.(x, y) = (0, 1): Angle with the x-axis: q = 90o = p/2
Þ cos q = cos p/2 = 0; sin q = sin p/2 = 1.(x, y) = (-1, 0): Angle with the x-axis: q = 180o = p
Þ cos q = cos p = -1; sin q = sin p = 0.(x, y) = (0, -1): Angle with the x-axis: q = 270o = 3p/2
Þ cos q = cos 3p/2 = 0; sin q = sin 3p/2 = -1.These turn out to show the extreme values of both sine and cosine functions. It is imperative to commit them to memory, along with several additional common angles. These common angles are most often described in the first quadrant only (acute angles); common angles in the rest of the quadrants are obtained from the acute angles by various elementary operations that we will describe in a separate article.
back to top Common Acute Angles and Right Triangles · The 30o/60o triangle · The 45o triangleAcute angles have measure less than 90o = p/2. There are two important right triangles (where one of the internal angles is exactly 90o = p/2 and the other two are acute) used as examples to study the trig functions of the acute angles within them. The first is the 30o/60o triangle, the second is the 45o triangle.
The 30o/60o triangle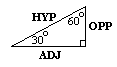
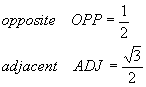
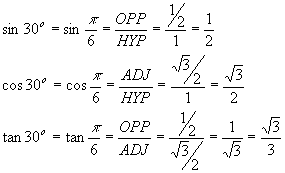
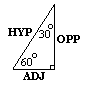
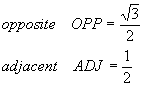
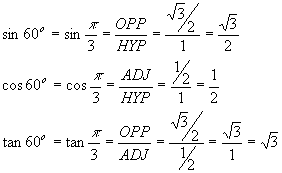
The last of the common triangles is the 45o = p/4 triangle, where both of the acute angles are the same:
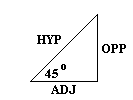
![]()
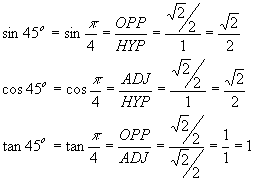
We mentioned above the definition of a right triangle - it contains a right (90o) angle with the other two acute. There are several other facts about triangles that may be helpful in later discussions.
