Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos

Introduction · Graph of the Cosine Function · Periodic Functions · Even Functions · Recommended Books

As we did with the sine function, we know that the x-coordinate of any point P on the circle is given by the cosine of the angle q between the positive x-axis and the line between the origin and P.

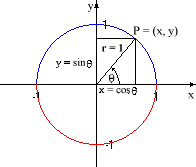
If one imagines the point P moving around the circle counter-clockwise starting from the point (0, 1) on the x-axis, the x-coordinate of P (which is x = cosq) goes from: x = 1 at q = 0; to x = 0 at q = 90^o = p/2; to x = -1 at q = 180^o = p; to x = 0 at q = 270^o = 3p/2; then back to x = 1 at q = 360^o = 2p. Notice that the starting and ending points are again the same; in other words, 0^o = 360^o = 0 = 2p (last two expressed in radians).

back to top

Were we to show several circuits around the circle as a graph of the horizontal displacement (x-coordinate) vs. the angle, it would look like this:

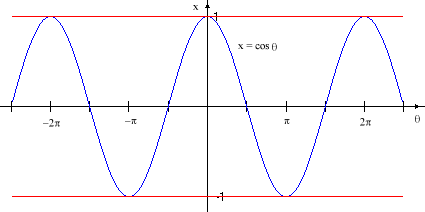
As with the sine function, the most obvious single feature of this graph is that it is periodic (a portion of the graph is repeated endlessly). In fact, the period of this function is T = 2p, so any portion of the graph that includes a full period repeats. In particular, the segments

and

both contain one full period, and either can be used as the repeating segment of the graph. As before with sine, we’ll use a basic period of the cosine function which suits our purpose best. If neither period has a distinct advantage over the other, either one can be used.

back to top

Like sine, cosine is a periodic function and has the same period as sine, T = 2p, so that

This is true for all real q. For example,

Again, it is only necessary to study a single period of the function in order to know its behavior everywhere. Since we are concerned with angles starting from the x-axis, we will use the period [0, 2p) as our sample period and ignore the entire rest of the real line (for now).

back to top

An even function f(x) has the property

Again, this is true for all real q. For example,

back to top

Recommended Books

Schaum's Outline of Trigonometry, 2/e

    The classic trigonometry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

 

 

 

back to top