ttlogo2.gif (23732 bytes)

Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos

Elementary Trigonometry Identities

Identities · Pythagorean Theorem · Addition and Subtraction Formulas · Recommended Books

Identities

With only the angles and their trig functions found previously, a large number of trig functions of other angles can be found with the use of a small collection of trig identities (also known as laws). An identity is an equation that is always true, so for example, the Pythagorean theorem

where x and y are the length of the sides, and r is the length of the hypotenuse of a right triangle, is always true. Thus this equation is an identity. There are equations that are not identities. For example, the equation

describes variables which are multiplicative inverses of each other; the equation is meaningless at x = 0, and so is not an identity.

Although there are many, many trig identities, we’ll concentrate on the use of just a few of the more useful ones, since the more obscure identities are always derived from the simpler ones. We’ll also make an effort so show how to derive these identities, in order to get some practice using algebra to assist our study of trig.

back to top

Pythagorean Theorem

This says the sum of the squares of the sides of a right triangle equals the square of the hypotenuse. Using the unit circle (where x = cosq, y = sinq and r = 1), this becomes

(Note on notation: the squares on the right hand side really apply to the entire function:

It is customary and much faster to write the powers of trig functions this way, and causes no confusion one the convention is known.)

Clearly, x and y (and so, by definition, cosq and sinq) must both be between –1 and +1:

Were these not true, the sum of the squares would exceed 1, and our identity would fail.

This identity is very useful, since we can find a cosine of an angle given the sine and vice-versa.

Example

Given that sin(p/6) = sin 30o = ½, find the cosine.

Solution

Solving the equation for cosq,

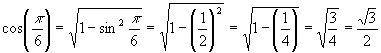
Since we are in the first quadrant, cos(p/6) >0 and we can drop the +/-. Thus,

Example

If sin 45o = cos 45o, find the value of both.

Solution

According to the identity, if we set a = sin 45o = cos 45o, we must have

and since the angle is again in the first quadrant,

back to top

Addition and Subtraction Formulas

Without proof, the identity for the sine of a sum is given by:

Sine addition formula

Example

Find sin 75o = sin (5p/12) given the above information.

Solution

Since 75 = 30 + 45, we are trying to find

 

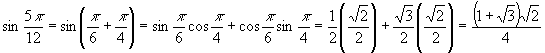
We can modify the above formula to handle subtraction by replacing –y for y:

Yielding:

Sine subtraction formula

Example

Find sin 15o = sin(p/12) using the above data.

Solution

Since 15 = 45 – 30, we should find

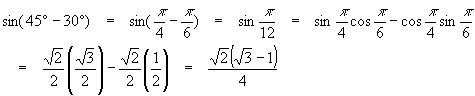
Note that sometimes degrees are more convenient to use than radians in planning these calculations, although radians are often better when computing the sines and cosines.

The corresponding formulae for calculating the cosines of a sum and difference are, respectively:

Cosine addition formula

Cosine subtraction formula

Example

Find the cosines of the angles from the two examples above.

Solution

Using the same ideas and applying the last two formulas,

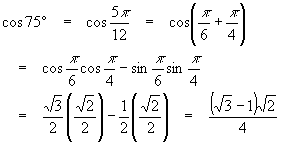
and

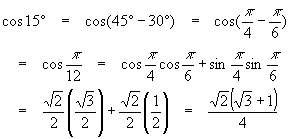
The attentive reader might have noticed that we found the trig functions for complementary angles, so that the numbers above verify that sin 15o = cos 75o and cos 15o = sin 75o !

back to top

Recommended Books

cover Schaum's Outline of Trigonometry, 2/e

    The classic trigonometry problem book - very light on theory, plenty of problems with full solutions, more problems with answers
 
 
 

back to top