
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Basic Math Operations Addition · Multiplication · Subtraction · Division · Identities · Powers and Exponentiation · Recommended Books AdditionCommutative Property of Addition · Associative Property of Addition · Distributive Property · Additive Identity: Zero
We'll assume the reader can add digits, so that 2 + 2 = 4 is not a surprise. In addition (heh!), we'll also assume that the fundamentals of "carrying" are not that big of a problem, and so most readers will immediately know how we did
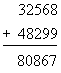
We're more interested here in the general properties of addition that impact algebra. With that in mind, let a, b and c be three real numbers. Then the following properties of addition turn out to be usable and important:
Commutative Property of Addition
![]()
(Addition is the same regardless of the order one adds the numbers, i.e., forwards addition is the same as backwards addition).
Examples
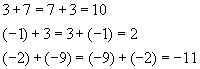
Note that negative numbers are sometimes enclosed in parentheses to avoid confusion between the sign of the number and the addition operation. This is merely a matter of style – many textbook writers use spacing to set off the difference instead.
Associative Property of Addition
![]()
(Addition of a list of numbers is the same regardless of which are added together first, i.e., grouping does not matter)
Examples
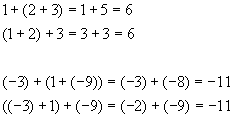
Commutative Property of Multiplication · Associative Property of Multiplication · Distributive Property · Multiplicative Identity
Again, we’ll assume that the basics of multiplication are well known, so that 2x2=2· 2=2*2=4. There are obviously several different notations in use, depending when one learns it and what context one learns it. We will use all of these notations, as well as another: when using variables, multiplication is assumed when symbols are merely written next to each other.
Multiplication follows the same two laws just described for addition.
Commutative Property of Multiplication
![]()
Examples
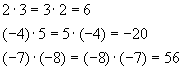
We are following the same convention as with addition. Note that just writing numbers next to each other is a poor idea because, for example, 32 can be confused with 3· 2. Thus, we need some sort of symbol to make the two distinct. There are several correct ways to do this – in other articles, we’ll make a lot of use of parentheses, so that 3· 2 will be written 3(2) or (3)(2). Experience with the notation will help make it very clear what is meant.
Associative Property of Multiplication
![]()
Examples
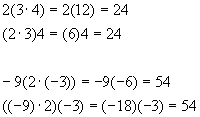
Please note that we do not have to limit ourselves to parentheses; the last computation could have been written
![]()
This looks a bit neater. Again, such things are a matter of style, and the reader is encouraged to use whatever bracketing makes the most sense and allows clear, proper ordering of calculations.
![]()
When both addition and multiplication appear in a single mathematical expression, this distributive law controls the operation. This is probably one of the most important laws in mathematics; getting it wrong guarantees bad calculations! The "reverse" is NOT CORRECT:
![]()
Examples
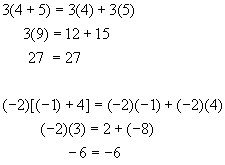
We’re going to define subtraction in terms of addition of the negative:
![]()
This means that subtraction is a shortcut or an abbreviation of the above addition operation. The "triple equals" sign used here means definition, and is meant to signify an operation that is always true. It is a stronger statement than a simple equals sign.
Examples
![]()
Subtraction is not in general commutative:
![]()
Example
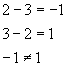
Nor is it in general associative:
![]()
Example
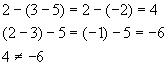
We’re going to define division in terms of multiplication of the inverse. Please see the discussion of multiplicative inverse below for more info. For now, suppose that a > 1 and that
![]()
The number b has a very important function – it is called the multiplicative inverse of a, also known as the inverse of a. Naively, we can write
![]()
but it should be pointed out that this is not really a definition. In order to properly define division, we would have to discuss rational numbers and how they work. Instead of doing that now, we’ll simply take it as given that the reader intuitively understands fractions. With this definition of inverse, we can tackle division:
![]()
Example
Suppose a = 2. Then
![]()
Note that the decimal expansion 0.5000… is the result of long division, a subject we are avoiding here (for a discussion, see the division article). We can "prove" that 0.5000… is the inverse of 2 by multiplying:
![]()
To the extent that this is rather unsatisfying, we must ask the reader to suspend disbelief. The mechanics of division are complicated, and deserve a separate article.
Now we’ll use this notion to do a division.
Example
![]()
Note that we expanded 6 into 2· 3 and canceled the 3’s. This is a bit sloppy, but again, our definition of division is intuitive rather than precise.
This definition of subtraction is based on the principle of the additive identity, also known as zero. Zero is neutral with respect to addition:
![]()
Another way to say this is:
![]()
What this allows us to do (among other things) is add the same quantity to either side of an equation.
Suppose we start with an equation we know is true:
![]()
If this is true then certainly
![]()
Therefore we can add the two equations to get
![]()
This is clearly and always true. The important point is we can always add the same thing to both sides. Similarly, since
![]()
we can always subtract the same thing from both sides of an equation.
As mentioned above, as long as a is non-zero, the relation between a and its multiplicative inverse is
![]()
Therefore, 1 is the neutral element for multiplication just as zero is the neutral element for addition. For any real number a,
![]()
The useful application of this is that we can take a true equation
![]()
and multiply it on both sides by the same thing, say b,
![]()
which will also be true.
A comment about division
We can get around a lot of the complications of division by simply replacing it with multiplication by the inverse. The difficulties inherent in this arise when we try to get an inverse of zero (undefined) or an irrational number (which does not have a repeating decimal expansion and so cannot be calculated by doing a long division). Irrational numbers won’t be much of a concern for now, since we can approximate most of them to as many decimal places as we need. In the rare case where we must deal with an irrational number exactly, we will just use a symbolic representation of it, for example
![]()
and just carry it along in our calculations.
Like subtraction, division is neither commutative nor associative.
For a little extra background on why division is a complicated subject, please see the articles on number systems and division.
Repeated multiplication of the same number are usually expressed as a power of that number, so that
![]()
and so on. The superscript or exponent is simply the number of times the number or base is multiplied times itself. Exponentiation follows some simple laws that follow directly from the above definition, the first being
![]()
For example,
![]()
Before going further, we need to define some "weird" exponents. Fractional powers are really combinations of roots and powers
![]()
so that, for example
![]()
Negative powers denote reciprocals:
![]()
For example,
![]()
With these definitions, we can say
![]()
for example,
![]()
We have now dealt with natural numbers, integers (i.e., including negative numbers) and rational numbers as exponents. So far we have not dealt with real number exponents, in particular irrational numbers. A proper treatment of this subject really requires calculus, and so we’ll avoid dealing with it at this time.
One further note that should be mentioned at this time is the nature of the base number. It should be clear that an irrational number in the base presents problems for practical calculation. For example, how does one calculate the following number?
![]()
Worse, how does one calculate a number such as this one?
![]()
The methods of advanced calculus provide ways to calculate such numbers to arbitrary precision. We won’t deal with how to do this here, but we will point out that modern calculators will do an adequate job of calculating these numbers, up to about 12 decimal places.

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students