Really, FOIL refers to multiplying the terms in parentheses to get the quadratic form. In that sense, we are actually UN-FOILing, but students are likely to know what we mean.

Here we take a quadratic, usually of the form

And try to put it in a form like

This amounts to guessing, so when it works, this is the fastest factoring method. We can try to systematize the method by multiplying the above out; the result is (skipping intermediate steps)

For most people, this is not very helpful. We will use this expression as a guide to guessing the numbers c₁, c₂, d₁ and d₂.

FOIL, of course, means: First, Outside, Inside, Last - the order of multiplication to expand the double parentheses form. The last two equations above show the beginning and end result of a FOIL calculation.

The easiest way to make sense of the guessing process is to consider examples and discuss them, constantly referring to the last equation in an effort to make the guesses consistent. We’ll start with the more involved examples and try to move towards easy special cases.

The worst possible case to consider is where all four numbers c₁, c₂, d₁ and d₂ are different. In addition, there are two "sub-cases" – ugly numbers and pretty numbers. Let’s try an example with four different, ugly numbers.

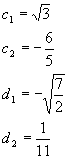
We’ll go backwards, produce the quadratic, and then comment about how this might be solved.

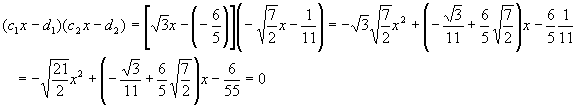
Pretty gross, huh? Even though we know what went into making this monster, looking at the quadratic makes it pretty hard to guess what factors went into it. The answer lies in using the magic of prime factorization – take every number and reduce it to a product of prime raised to various powers, then look for clues like repeated factors. We’re actually lucky with this example, since all the original factors are products of primes and there are no common factors (another complicating issue – we’ll blow this off and assume you have the sense to divide out all common factors).

Let’s pretend we are seeing the quadratic for the first time, and that it has been re-arranged somewhat to

throw us off.

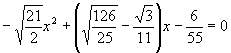
The first thing to do is factor all non-prime numbers into products of primes.

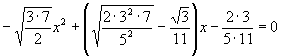
Next, write the form we are looking for immediately below

We have (matching coefficients of like powers of x)

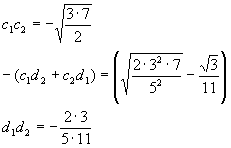
We can make a few conclusions already. The square root of 3 is probably one of the c’s, since it only appears where there are c terms. The 11 in the denominator only appears where there are d terms, so it is likely one of the d terms. It is also reasonable to conclude that the two terms on the right hand side in the middle expression correspond to the two different terms on the left hand side. Moreover, we don’t care if we mix up the "1" and "2", so long as we do it consistently (to be more precise, exchanging "2" for "1" everywhere is OK – the subscripts are arbitrary labels, but it is a big error to exchange the labels in one part of this calculation and not another – that will lead to inconsistent results, and we’ll never find an answer). Last, if we get a sign (+ or -) wrong, but otherwise our calculations are correct, we’ll be OK, since the sign will either show up elsewhere if it matters, or else it doesn’t matter (e.g., signs don’t matter here: (1)(2) = (-1)(-2) = 2).

Let’s take a guess and set

and see where this assumption leads. Direct matching with the middle term leads to the reasonable conclusion that

From the d₁, d₂ term,

From here, it is easiest to use the first relation (the c₁, c₂ term) to get the last remaining number

Now that we have extracted all four coefficients, we can say we have factored the equation. If we want to claim we have actually found the two solutions, we have an extra couple of steps. Set each term in turn to zero

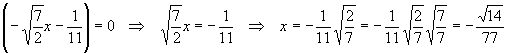
Please note that we bothered to rationalize the denominator in both calculations, something that always should be done (dividing by an irrational number is theoretically possible, but practically impossible). We avoided rationalizing before the very last step, which is OK, but when radicals appear in the denominator of our answers, this must be fixed.

A lazy person could very well argue after all this that the quadratic formula is quicker. It is true, but the value of the above process is practicing looking at a set of equations for clues, using those clues to get answers, and then checking the answers to see if they make sense. There really is no substitute for an intimate connection with the math, and doing a guess method like the one outlined above is a great way to get very good at algebra – just organizing the calculation to avoid silly mistakes is a challenge. Remember, the example above was deliberately selected to be as ugly as possible!

This should be easier than the above example. The equation we need to solve is

Let’s drag in our coefficients again, as a memory and organizational aid. In this case, direct comparison shows that (immediately converting to prime factorization)

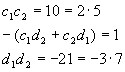
We have a pretty obvious solution right at hand:

There is some uncertainty about the signs as noted. The thing to do is choose a definite value for one of the coefficients, then go through the equations to get all the others consistent. If that works, we’ll be off by at most a minus sign (since the entire expression is equal to zero, this will not matter). So, let’s choose the most obvious possible value for the first constant.

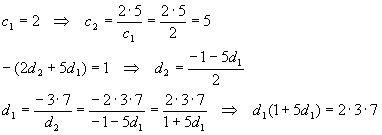
While this is another quadratic, we already have an idea what the solution must be, so let’s try putting in d₁ = 3 and see what happens.

That is not correct, so we’ll try the other candidate, d₁ = -3:

This worked. We have only d₂ to go:

Now we check the work by assembling the coefficients and multiplying:

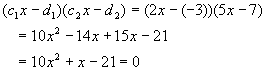
Which is our original quadratic.

We still haven’t found the roots! This is important to remember – in the most general case, finding all the constants is not the same as getting the roots! Fortunately, it’s a smooth ride from here…

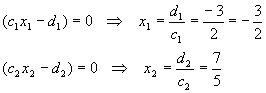
Note: There is an intermediate case, where only one of c₁ or c₂ is 1 and the other is different than 1, but I classify this as four separate numbers, since it is just as difficult as the preceding case.

The usual "reverse FOIL" commonly discussed in high-school level math covers the case where the two c’s are equal to 1, so that the guessing involves just the d’s, a much easier case. We’ll talk about it in the same context as the above examples, again because we’re trying to show that the mechanics are pretty much the same for all these problems.

The first thing to do is to see the effect of setting the c’s to 1 on our guide equations:

When multiplied out, this looks like:

We’ll do a couple of examples to show how much easier this makes it to guess the solutions.

Find the roots

We need two numbers whose sum is –3 and whose product is –10. Let’s guess 2 and –5. Plugging them in gives

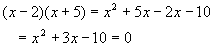
Since we got our original quadratic back, we’re done.

We could have tried to use the guide equations in the last example

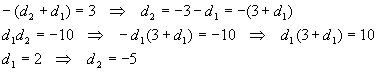
This is a bit more systematic, but still involves guessing. The previous method seems more straightforward – just guess and plug in to see if the guesses were right.

Find the roots

We’re looking for two numbers whose sum is –22/21 and whose product is 5/21. Since these numbers are a bit ugly, we’ll resort to using the guide equations

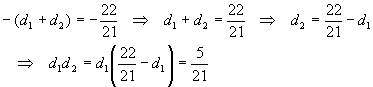
This is satisfied by

Which forces

Plugging these back into the quadratic gives

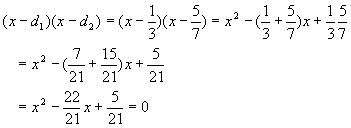
It should be obvious from this example that lots of experience working with numbers (i.e., arithmetic) is really handy. Rather working a ton of fairly useless arithmetic calculations, we suggest you use the opportunities presented in the course of working algebra problems like the one above to give yourself more experience. There is no harm (and much benefit) from jotting down a few notes here and there when you find an interesting insight into the numbers you are working.

There are an infinite number of different quadratic equations. These notes present you with three very different methods of solving them (FOIL in this document, completing the square and the quadratic formula). More importantly, we have sketched a way of classifying quadratics in each case. By working many problems (perhaps solving a given quadratic each of the three ways to see which is best for a particular case), you’ll eventually develop intuition about which method is most likely to work "best" for a new quadratic you have never seen before.