
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Synthetic DivisionBasic Process of Dividing Polynomials · Limitations · Remainders · Examples · Recommended Books
Basic Process of Dividing Polynomials
Elsewhere, we introduced the concept of synthetic division. Now we are going to amplify the concept and develop it more fully. The basic idea is to take a "big" (higher order) polynomial and divide it into a "small" (lower order) polynomial. If it divides evenly, we have in effect partially factored the polynomial.
For example, let’s divide the following expression:
![]()
We’ll take the example step-by-step. The larger polynomial is the dividend, the smaller is called the divisor. First, set up the division:
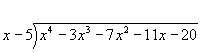
Looking at the first term in the dividend, we ask, "How many times does the first term of the divisor (x) need to be multiplied to get the first term of the dividend (x4)? The answer is x3. Write x3 on top of the bar above the x4 term, multiply both terms of the divisor by x3, and write each result below the dividend term with the same power of x. Subtract:
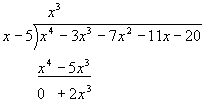
Notice that the x4 terms cancel, and that –3x3 – (–5x3) = 2x3. For the next step, we bring down the next term (-7x2), so the new dividend term is 2x3 - 7x2. Again examining the highest order terms, we notice that 2x3 / x = 2x2, so our next term is 2x2:
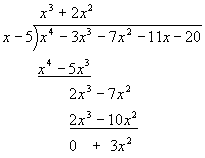
Now, bring down the next term (-11x) and do the next division 3x2 / x = 3x:
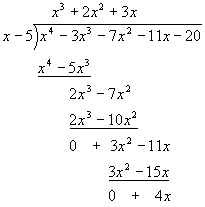
Last step: 4x / x = 4, so we put a 4 on top and perform the final division step:
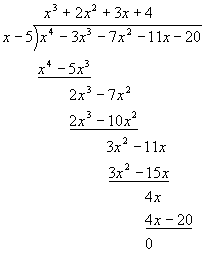
The remainder is zero, so we have found that x = 5 is a zero of the polynomial and a root of the equation.
When you actually do these problems, you will do a single calculation that looks like the last figure above. If the dividend is not evenly divided by the divisor, the space where the 0 goes at the end will be occupied by a number R, the remainder (see an example of a remainder problem later). The above process greatly resembles ordinary long division, and is in fact a generalization of ordinary long division, where x is always 10.
The above process can be streamlined. Compare the following to the above.
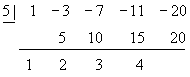
Here’s how the process works. The first line is the divisor (just the coefficient of x0 = 1) inside the angle bracket, followed by the dividend, stripped of all powers of x, but written in order of decreasing powers of x. Missing powers of x must be represented by a zero in that place. The second line is the working line, where intermediate calculations are written one at a time. The bottom line is the quotient. The places in the quotient represent powers of x "one fewer" than the corresponding entry in the dividend directly above.
The first coefficient is just brought down to the third line, corresponding to the operation x4 / x = x3. The divisor number in brackets (the 5) then multiplies this number. The result (5) is written below the next place on the second line. Now, the numbers in this column are added (-3 + 5) and the result (2) is written below on the third line. Multiply this new result (2) by the divisor (5) and write the new intermediate result (10) in the next available space on the second line. Add again (-7 + 10) and write the result (3) below on the third line. Multiply this new result (3) by the divisor (5) and write the intermediate result (15) in the next available slot on the second line. Add again (-11 + 15) and write the result (4) below on the third line. Multiply this last result (4) by the divisor (5), write the result (20) below in the last slot on the second line.
Add for the last time (-20 + 20) and the result is zero – so the divisor divided the dividend evenly.
We then can take the third line and translate it into the quotient polynomial:
![]()
The advantage of this method is that it is much quicker – a little practice reduces it to a rote process that can be very quickly executed. Speed of computation matters in factoring polynomials, since the trial and error nature of the process often requires that many possible roots be tried. Several quick calculations can be fit on a single page, a convenience when doing large numbers of computations.
As presented, synthetic division is only good for divisors of the form (x - a). Since we are usually looking for factors of this form, this is not really a serious limitation. In particular, the method is not really suited for factors (divisors) with three or more terms, such as x2 + x + 2.
Suppose we took the above example and modified the dividend to read
![]()
If we performed the same division by (x – 5), we’d wind up with nearly the same synthetic division:
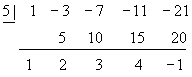
The difference is in the last term on the third line – the remainder is no longer zero. The quotient must now read
![]()
This has an important consequence. The original polynomial, now considered as a function, can be written
![]()
What happens if we substitute x = 5 into this equation? First, we should re-write it a bit:
![]()
Now we can substitute x = 5:
![]()
So, if a division of a polynomial results in a non-zero remainder, substituting the x that makes the divisor zero results in the value of the polynomial equal to the remainder!
Divide using synthetic division
![]()
Solution
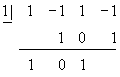
So the quotient is
![]()
Divide by synthetic division
![]()
Solution
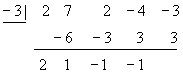
So the quotient is
![]()
Find the quotient
![]()
Solution
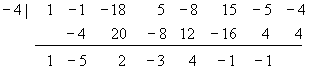
So the quotient is
![]()
Suppose the previous division was
![]()
Find the quotient and evaluate the dividend at x = -4.
Solution
Set up the division as before, with the slightly altered result:
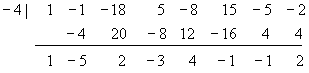
The quotient is now
![]()
The original polynomial can now be rewritten
![]()
Note that this is the same as
![]()
Therefore,
![]()
Which is just the value of the remainder!

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students