
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Quadratic Formula Examples
The Quadratic Formula · Case I - Two real, distinct roots · Case II - One real root · Case III - Two complex conjugate roots · Recommended Books The Quadratic Formula![]()
The portion of the formula under the radical is called the discriminant, and determines which of the three cases is under consideration.
Case I - Two real, distinct roots
In this case we have
![]()
So there are two different roots, both real numbers.
Example
Find the roots (solve for x):
![]()
Solution
Plug the numbers into the quadratic formula
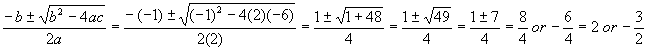
As a check, plug these solutions into a generic (parentheses or FOIL) form
![]()
Multiplying the last expression by 2 yields the above quadratic.
Example
Find the roots (solve for x):
![]()
Solution
Plug into the quadratic formula
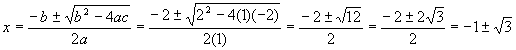
Thus the two roots are
![]()
Do a FOIL check to make sure these are correct
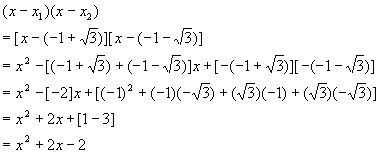
This is a good calculation to go through carefully, since it contains lots of opportunities for errors. Sticking to the FOIL method helps, as does proper use of parentheses and brackets. Instructors love putting these types of problem on exams, since they really test the students' organizational skills and attention to detail.
This is the case where the discriminant is zero
![]()
…and so the expression under the radical vanishes, leaving nothing after the +/-. This corresponds to the graph having only the vertex touching the x-axis, so there is exactly one real root.
Example
Find the roots (solve for x):
![]()
Solution
Plug into quadratic equation:
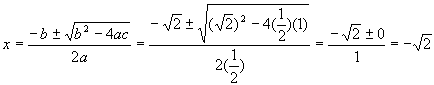
Now do a check:
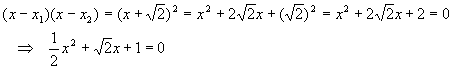
…upon division by 2. Note that it is very difficult to see that this equation is a perfect square by inspection.
Example
Find the roots (solve for x)
![]()
Solution
Plug into quadratic formula:
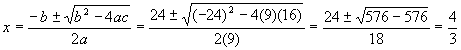
As a check, multiply out the square:
![]()
Case III - Two complex conjugate roots
A few short comments about complex numbers are appropriate here. As we saw in the Quadratic Theory section, some quadratics do not cross the x-axis at all. For example, the quadratic
![]()
never gets closer than 1 to the x-axis, and so has no real zeros at all. However, if we try to solve it anyway,
![]()
The symbol 'i' is an abbreviation for the square root of minus one, and is called the imaginary unit. Any number that includes this symbol is a complex number (not a real number). For the time being, the only thing we care about i is that i2 = -1. A general complex number is usually written
![]()
where a and b are real numbers (the real part and imaginary part respectively). Every complex number has a complex conjugate
![]()
where the sign of the imaginary part is reversed. Complex conjugate pairs of numbers are interesting because their products are always real:
![]()
In fact, if either a or b is non-zero, this product is positive.
Example
Solve for x
![]()
Solution
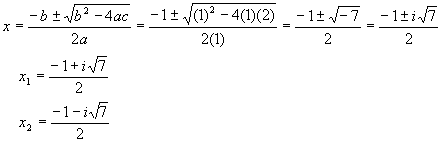
Plug into the FOIL to verify
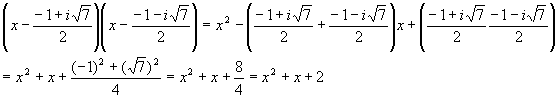
Note that we used the results from the product of complex conjugates to simplify the product of the roots.
Example
Solve for x
![]()
Solution
Plug into quadratic formula
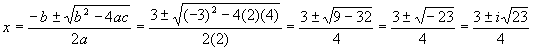
And then do a FOIL to check
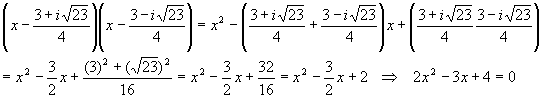

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students