
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Linear Functions and Straight LinesLinear Functions: Slope-Intercept Form · Slope · Intercept · Point-Slope Form · Examples · Recommended Books
Linear Functions: Slope-Intercept Form
Linear functions describe straight lines and have the general form
![]()
The number m is called the slope and determines the tilt of the line, while b is called the y-intercept, the point on the y-axis where the line crosses at x = 0. This form of a linear equation is often called slope-intercept form. A typical graph of one of these functions looks like this:
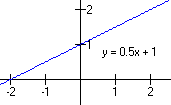
The slope is calculated from knowing any two distinct points on the line, (x1, y1) and (x2, y2)
![]()
If the points are distinct, then the x coordinates cannot be the same and so zeros in the denominator are avoided.
The y-intercept can be calculated from any point if the slope is known. Since for any point (x1, y1)
![]()
we must then have
![]()
Given any two distinct points on the line, (x0, y0) and (x, y), we can set up two versions of the equation for the line
![]()
Subtracting, we get
![]()
This is the point-slope form.
Slope-Intercept and Point-Slope Forms from Two Points · Y-Intercept From Point-Slope Form · Intercepts and Slope-Intercept Form · Crossing Lines · Perpendicular Lines · Parallel Lines
Example - Slope-Intercept and Point-Slope Forms from Two Points
Find the equations in slope-intercept and point-slope form for the line that passes through the points
![]()
Solution
First calculate the slope:
![]()
Then take one of the points and calculate the intercept:
![]()
As a check, let’s do the same calculation with the other point:
![]()
We got the same result with both points, a good indication that the calculations are correct. The equation of the line in slope-intercept form is
![]()
and the equation in point-slope form is
![]()
Example - Y-Intercept From Point-Slope Form
Given the following equation of a line in point-slope form:
![]()
Find the y-intercept.
Solution
There are two ways to do this problem. The first is to multiply out the right-hand side of the equation and subtract 1 from both sides:
![]()
So we now know the intercept is –7. The other way to do this problem is to use the intercept formula:
![]()
We arrived at the same answer.
Example - Intercepts and Slope-Intercept Form
The y-intercept of a line is 3 and the x-intercept is 2. What is the equation of the line in slope-intercept form?
Solution
The y-intercept of a line is the y-coordinate where x = 0. Therefore, if the y-intercept is 3, the point on the line is (0, 3). In similar fashion, the x-intercept is the point on the x-axis where y = 0. Thus, if the x-intercept is 2, the point is (2, 0). With this information, we can apply the methods of the first example. First, calculate the slope:
![]()
Now, we don’t have to calculate the y-intercept because it was given as 3! The equation of this line is:
![]()
Example - Crossing Lines
At what point do the following two lines cross?
![]()
Solution
The lines cross at a single point, so the lines must have the same x and y coordinates at that point.
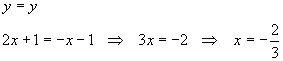
Now that we have the x-coordinate, we can use either equation to find the y-coordinate:
![]()
Now we have both coordinates, so the answer is:
![]()
Example - Perpendicular Lines
Find the line perpendicular to
![]()
that crosses this given line at (1, 17/6).
Solution
This example requires a formula for perpendicular lines, whose slopes are related by
![]()
So for our second (perpendicular) line, the slope is
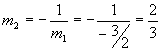
We know that the point (1, 17/6) belongs to both lines, so we might as well use it. Plugging into the formula for the y-intercept,
![]()
Thus the equation for the perpendicular line is
![]()
Example - Parallel Lines
Find the line parallel to the line
![]()
which passes through the point (-5, 1).
Solution
Parallel lines have the same slope, so we already know that m = 2. Plugging in to get the intercept yields
![]()
So the final line is
![]()

The classic algebra problem book - very light on theory, plenty of problems with full solutions, more problems with answers

A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students