
Technical Tutoring Home · Site Index · Advanced Books · Speed Arithmetic · Math Index · Algebra Index · Calculus Index · Trig Index · Chemistry Index · Gift Shop · Harry Potter DVDs, Videos, Books, Audio CDs and Cassettes · Lord of the Rings DVDs, Videos, Books, Audio CDs and Cassettes · Winnie-the-Pooh DVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys · STAR WARS DVDs and VHS Videos
Chemical Equilibrium Examples II Reaction Quotient · Temperature Changes · Pressure Changes · Chemical Equilibrium Definitions · Chemical Equilibrium Examples I · Solubility Products · Chemistry Index · Math Index · Recommended Books · Advanced and In-Depth Books · Site Index Reaction QuotientExample
: Use of reaction quotient to predict direction of a reactionWhich way will each mixture react? Assume Kc = 96.2 M-1 for the reaction A + B <-> C.
- Case 1: [A]0 = 0.0933 M, [B]0 = 0.123 M, [C]0 = 0.389 M
- Case 2: [A]0 = 0.0233 M, [B]0 = 0.0123 M, [C]0 = 0.999 M
- Case 3: [A]0 = 0.0333 M, [B]0 = 0.0333 M, [C]0 = 0.1067 M
Solution: Calculate Qc for each case and compare to Kc = 96.2 M-1 . For case 1,
![]()
Since Qc < Kc , (not enough product or too much reactants) this reaction will move forward. For case 2,
![]()
Since Qc > Kc , (not enough reactants or too much product) this reaction will move backward. For case 3,
![]()
Since Qc = Kc , this system is at equilibrium and will stay as it is.
Our fourth type of equilibrium problem, temperature changes, requires discussion of thermodynamics. By referring to the standard enthalpy of formation tables in any freshman chemistry book, we can find the change in enthalpy for the chemical reaction, and use this value to predict how the reaction equilibrium changes with temperature.
As a review, let’s calculate the standard enthalpy (at 298K = 25oC) for the reaction we have been considering so far:
![]()
The standard enthalpies of formation for each component are:
Using the standard (products – reactants), we get:
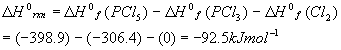
This number will be used below.
The equilibrium constant is a function of temperature, which is expressed in the Van’t Hoff equation:
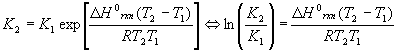
Either version may be used, depending on which is easier to solve for the desired variable. Note that there are two K’s and two T’s, to be understood that K2 goes with T2 and K1 goes with T1 . The enthalpy of reaction DHorxn is considered constant. In reality, this number varies some with temperature, so this equation is an approximate form of a much more complicated equation and should be used over relatively small temperature ranges (no more than +/- 200K about 298K). Also, please note that exp(x) = ex.
Note that there are five different variables in this equation: DHorxn , T1 , T2 , K1 and K2 . Since the equation can be solved for any one of them (more on the T’s later), this equation alone can generate at least three completely different kinds of problems, solving for DHorxn , K’s and T’s.
Example: Finding a new equilibrium at a different temperature
Suppose the above reaction, abbreviated again to
![]()
Is at equilibrium at 400 K. As before, the equilibrium constant is 96.2 M-1 at this temperature. The equilibrium concentrations are
If we take this system and change the temperature to 298 K, what will be the new equilibrium concentrations?
Solution:
The first thing to do is find the value of Kc at 298 K. To do this, use the first version of the Van’t Hoff equation and the value of
DHorxn we calculated above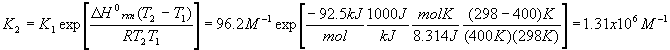
When we change the temperature, the old Kc becomes the new Qc because the reaction is no longer at equilibrium. Our new Kc is much larger after the temperature change, and so we expect the equilibrium to shift to the right (forward reaction predominates).
We can now set up a new start-change-finish diagram:
| Component | A | B | C |
| Start | [A]0 = a | [B]0 = a | [C]0 = b |
| Change | - x | - x | + x |
| Finish | a - x | a - x | b + x |
So,
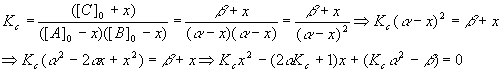
And we have
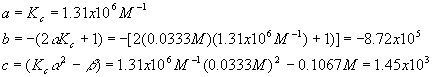
Plugging these values into the quadratic equation gives
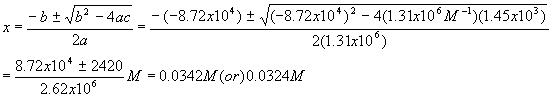
The first solution gives a negative (physically impossible) value for [A] and [B] so we use the second solution
If these values are plugged in to check
Kc we get an answer which is terribly far from our original value,Kc = 1.72x105. This should not be too surprising, given what we have seen before and the fact that when we calculated [A] and [B], we took the difference between two small numbers that were close together.
This type of calculation is a good candidate for trial and error. Let’s summarize what happens if we do that. The algebra above yields
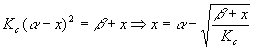
Starting with x = 0, we got the successive values 0.03301, 0.03297, 0.03297 and stopped there. Now,
Plugging these values into the definition of
Kc yielded 1.31x106, as expected. The moral is: watch out for situations like this, which will ruin your precision! The difference of two small numbers which are close together is always such a case. Pressure ChangesThe last theoretical point we need to cover is that of pressure changes. Since by Le Chatelier's rule, the system tries to undo what we do to it, we can state the pressure rule simply: increases in pressure favor the side of the reaction with the fewest moles in the gas phase. In our example reaction, the product side is favored when pressure is increased. It makes the most sense to do these problems in terms of partial pressures, although they can be done in concentrations as well.
Example: Calculation of KP from Kc
If the value of Kc at 400 K is 96.2 M-1, what is the value of KP ?
Solution:
From the definitions,
![]()
Example: Calculation of partial pressures from concentrations
Suppose as before
What are the corresponding partial pressures and the total pressure? The temperature is again 400 K.
Solution:
For each component, PX = [X]RT, so
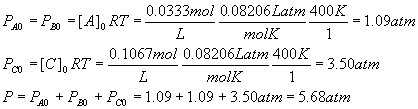
Example: Effect of pressure change on equilibrium
Suppose the above system suddenly experienced a pressure drop to 4.00 atm at a constant temperature of 400 K. What would the new equilibrium partial pressures become?
Solution:
This problem is interesting because if the total pressure suddenly changes, so do all the partial pressures.
What does not change (until the system goes to equilibrium, which it has not done immediately after the pressure change) is the relative amounts of each component, in other words, the mole fractions (see definitions).
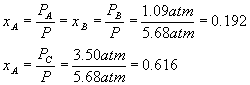
After the pressure change,
![]()
Equilibrium will cause a shift to the left, in order to make more gas and so more pressure, since we reduced the pressure and the system tries to undo what we did to it. Setting up a start-change-finish diagram,
| Component | A | B | C |
| Start | PA0 = a | PB0 = a | PC0 = b |
| Change | + x | + x | - x |
| Finish | a + x | a + x | b - x |
This gives
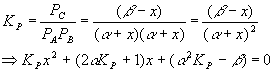
Plugging in the numbers for each coefficient yields
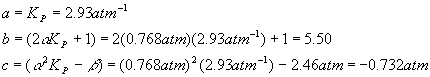
And so the quadratic solutions become
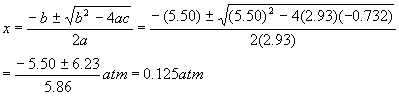
Rejecting the obviously impossible negative solution. Therefore, the pressures are:
Plugging these values into as a check gives
![]()
So we can be confident our answer is correct.
All other chemical equilibrium problems are variations of the techniques shown in these notes, or combinations of these techniques. By practicing with these problems until new problems can be done easily and without errors (in other words, the check you do at the end agrees with your results), you will be able to perform well on your next chemistry exam.

$14.35 · The classic chemistry problem book - very light on theory, plenty of problems with full solutions, more problems with answers

$8.05 · A simplified and updated version of the classic Schaum's Outline. Not as complete as the previous book, but enough for most students